섀넌, 확률, 그리고 켈리 기준 (Shannon, Chance, and The Kelly Criterion)
벨 연구소(Bell Labs) 과학자인 클로드 섀넌(Claude Shannon)은 정보 이론(information theory)—본질적으로 정보를 전송하는 데 필요한 속성과 시스템—을 개발한 것으로 잘 알려져 있다. 섀넌 이전에는 대부분의 엔지니어가 메시지의 의미에 초점을 맞추어 정보 문제를 이해하려고 했습니다. 섀넌의 통찰은 정보가 확률(chance)과 관련되어 있다는 것이다.
작가 윌리엄 파운드스톤(William Poundstone)이 언급했듯이, "정보는 발신자가 수신자가 이미 모르거나 예측할 수 없는 무언가를 말할 때만 존재한다. 진정한 정보는 예측할 수 없기 때문에, 본질적으로 룰렛 휠의 회전이나 주사위 던지기처럼 일련의 무작위 사건과 같다."
예를 들어, 파운드스톤은 아내가 남편에게 "샴푸(shampoo)"를 사 오라고 요청하는 TV 광고를 언급한다. 남편은 아내의 말을 오해하고 "샤무(Shamu)"라는 범고래를 데리고 나타난다. 아내의 요청이나 남편의 오해는 놀랍지 않다. 광고가 우리의 주의를 끄는 이유는 남편이 추가 정보 없이 매우 희박하고 예측 불가능한 요청에 따라 행동했기 때문이다.
섀넌에게 있어 메시지의 압축 불가능한(incompressible) 부분은 예측 불가능성과 관련이 있었다. 메시지의 발생 확률이 낮을수록, 더 많은 대역폭(bandwidth)이 필요합니다. "샤무"를 데려오라는 요청은 일상적인 "샴푸" 요청보다 의심할 여지없이 더 많은 대역폭을 요구한다.
섀넌의 이론은 또한 모호성(equivocation)—메시지가 틀릴 확률—을 고려하며, 정보 전송률을 결정하기 위해서는 채널 용량에서 모호성을 빼야 함을 보여준다. 더 신뢰할 수 있는 정보는 주어진 채널 용량에 대해 더 높은 정보 전송률로 이어진다. 오늘날 우리가 사용하는 전화, 텔레비전, 인터넷을 포함한 대부분의 정보 채널은 섀넌의 아이디어를 사용하여 작동하고 있다.
최적 베팅 규모와의 연결
이 모든 것이 최적의 베팅 규모와 어떤 관련이 있을까? 섀넌의 벨 연구소 동료였던 존 켈리(John Kelly)는 정보 이론의 아이디어가 도박에 응용될 수 있음을 알아차렸다. 베팅 환경에서 정보는 시장이 아직 알지 못하는 것인데, 모호성의 개념과 일치하게, 진정한 정보 역시 확률적이다.
켈리는 자신이 우위(edge)를 가지고 있는 시스템, 즉 시장의 기대와 다른 일련의 기대를 가지고 있는 시스템을 상상했다. 그리고 섀넌의 연구를 기반으로, 장기적으로 자본을 극대화하기 위해 자본금 중 정확히 얼마의 비율을 베팅해야 하는지를 보여주는 공식을 개발했다. 이 이론에 따르면 최대 수익률은 시장이 모르는 무언가를 알고 있을 때 나온다.
우리는 켈리 공식을 여러 가지 방식으로 표현할 수 있다. 파운드스톤의 설명에 따르면 다음과 같습니다.
여기서 '우위(edge)'는 그 금융 거래의 기대값(expected value)이며, '배당률(odds)'은 승리했을 때 얼마를 따게 될지에 대한 시장의 기대를 반영하고, f는 여러분이 베팅해야 할 자본금의 비율을 나타낸다. 주의할 점은 효율적인 시장에서는 배당률이 성공 확률을 정확하게 나타내기 때문에 우위(edge)가 없다는 것이다.
따라서 시장의 정보에 기반한 베팅은 (베팅에 드는 비용을 제외하면) 기댓값이 0이며, 최적 베팅 비율인 도 0이다. 켈리 공식을 사용하여 서두에 제시했던 동전 던지기 문제의 답을 구해보자. 앞면이 나오면 2달러를 따고, 뒷면이 나오면 1달러를 잃는 지급 방식은 2 대 1의 배당률을 시사한다. 우리가 공정한 동전을 다루고 있기 때문에, 던지기 결과는 1 대 1로 나올 것임을 알고 있다. 따라서 우리는 시장이 알지 못하는 것을 인지하고 있으며, 앞면이 지급 방식이 시사하는 것보다 더 자주 나올 것으로 기대할 수 있다.
이 공식을 풀어보면, 우위(edge)는 (기대값: 50% )이고, 배당률(odds)은 다(승리했을 때 따는 금액). 따라서 최적의 베팅 금액은 매 라운드마다 자본금의 25% 임을 알 수 있다. 다르게 말하면, 25%를 베팅하는 것이 평균적으로 다른 어떤 베팅 전략보다 더 큰 부의 축적으로 이어질 것이다.
$0.50 / $2.00 = f = 25%
도표 2는 40라운드 동안 값의 범위에 따른 자산의 분포를 보여준다. 너무 적게 베팅하면 상당한 금액을 테이블 위에 놓아두는 것이 되며, 너무 많이 베팅하면 거의 확실한 파산으로 이어질 것이다. 후자는 강조할 필요가 있다. 즉, 손실 확률이 있다면, 기댓값이 양수인 경제적 거래일지라도 너무 많이 베팅하는 것은 기대되는 부를 감소시킨다. 이러한 과도한 베팅은 다수의 유명 헤지펀드가 몰락한 원인일 것이다.
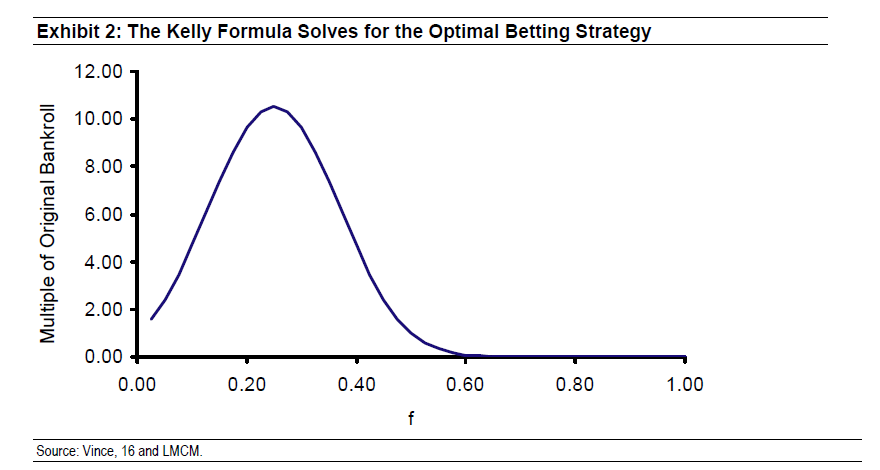
비록 기본적인 예시일지라도, 이 설명은 모든 종류의 투자자들에게 두 가지 중요한 핵심을 시사한다.
- 현명한 투자자는 우위(edge)를 갖고 있다(시장의 견해와 다른 관점).
- 투자 아이디어가 나타났을 때, 투자자는 가치를 극대화하기 위해 자본을 적절히 배분해야 한다.
켈리 공식은 켈리 기준(Kelly Criterion) 또는 켈리 시스템(Kelly system)으로 알려진 더 큰 개념으로 이어진다. 정보 이론에 기반을 둔 켈리 기준은 투자자가 가장 높은 기하 평균 수익률(geometric mean return)을 가진 투자 대상을 선택해야 함을 알려준다. 이 전략은 평균-분산 효율성에 기반한 전략과는 구별된다. 하지만 중요한 점은, 평균-분산 모델의 산술 평균과 분산을 사용하여 기하 평균을 계산할 수 있다는 것이다.
수학자이자 투자자인 에드 소프(Ed Thorp)는 아마도 켈리 기준의 가장 눈에 띄는 옹호자이자 성공적인 투자자일 것이다. 1960년대 초, 소프는 카드 게임 블랙잭에서 플레이어의 승률을 높이는 카드 카운팅 시스템을 개발했고, 이를 켈리 시스템으로 보완하여 부의 축적을 최적화했습니다. 소프는 나중에 Princeton-Newport Partners를 공동 설립하여, 다양한 투자 전략을 통해 20년 동안 20%의 연평균 복합 수익률과 6%의 표준편차를 달성했다.
자신의 저서 '도박의 수학(The Mathematics of Gambling)'에서 소프는 켈리 시스템의 매력적인 특징들을 다음과 같이 설명한다.
1. 파산 확률이 "작다"
켈리 시스템은 비례 베팅에 기반하므로, (자금이 무한히 분할 가능하다고 가정하면) 모든 자본을 잃는 것은 이론적으로 불가능하다. 그럼에도 불구하고, 상당한 자본 감소(significant drawdown)의 적은 가능성은 남아 있다.
2. 다른 시스템보다 자본금을 더 빨리 늘릴 가능성이 매우 높다
비슷한 매력적인 기회가 계속 나타난다면, 이 시스템은 다른 시스템들을 정해진 배수만큼 초과하는 자본금을 생성할 확률이 높다.
3. 특정 승리 수준에 도달하는 평균 시간이 가장 짧은 경향이 있다
재정적인 최종 목표를 염두에 두고 지속적인 기회가 있다면, 켈리 시스템은 다른 시스템보다 더 짧은 시간에 목표를 달성하도록 할 가능성이 높다.
요컨대, 켈리 시스템은 이론적으로 건전할 뿐만 아니라 투자자들에게 유용함이 입증되었다. 그러나 이러한 접근 방식을 가장 열렬히 지지하는 사람들(정보 이론가, 수학자, 도박사, 트레이더) 중에는 주류 경제학자가 포함되지 않는다. 이제 우리는 켈리 시스템의 몇 가지 실제적인 제약 조건들을 살펴보고, 켈리 시스템과 평균-분산 효율성을 대조해 볼 것이다.
Reference
Michael Mauboussin. Size matter. Mauboussin on Strategy. Legg Mason Capital Management. Feb 1. 2006
투자 규모 문제 1편 보기
2025.10.08 - [투자] - 투자 규모 문제 1편. 마이클 모부신
투자 규모 문제 1편. 마이클 모부신
켈리 공식(Kelly Criterion)과 자금 관리의 중요성"정보를 가지고 좋은 판단을 내릴 수 있는 회사에 상당한 지분(a substantial stake)을 투자하는 것에 비해, 내가 좋은 판단을 내릴 정보가 없는 수많은 다
blueorbit.tistory.com
'투자' 카테고리의 다른 글
| 투자 규모 문제 1편. 마이클 모부신 (1) | 2025.10.08 |
|---|---|
| 후회 없는 투자 (2) | 2025.08.31 |
| 패리뮤추얼 베팅(Parimutual betting) (3) | 2025.08.28 |
| 지분이익 관점에서 본 장기 투자 전략 (2) | 2025.08.12 |
| 찰리 멍거가 말하는 가치 투자의 본질 (4) | 2025.08.11 |



